Transformer 是一种基于自注意力机制的深度学习模型，最初由 Vaswani 等人在 2017 年的论文《Attention is All You Need》中提出。Transformer 模型突破了传统序列模型（如 RNN 和 LSTM）的局限性，在自然语言处理（NLP）领域取得了巨大的成功，广泛应用于机器翻译、文本生成、问答系统等任务。

Attention机制

注意力模型 Attention 的本质思想为：从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上，忽略不重要的信息。

注意力模型从大量信息 Values 中筛选出少量重要信息，这些重要信息一定是相对于另外一个信息 Query 而言是重要的，例如对于上面那张婴儿图，Query 就是观察者。也就是说，要搭建一个注意力模型，我们必须得要有一个 Query 和一个 Values，然后通过 Query 从 Values 中筛选出重要信息。

通过 Query 这从 Values 中筛选出重要信息，简单点说，就是计算 Query 和 Values 中每个信息的相关程度。

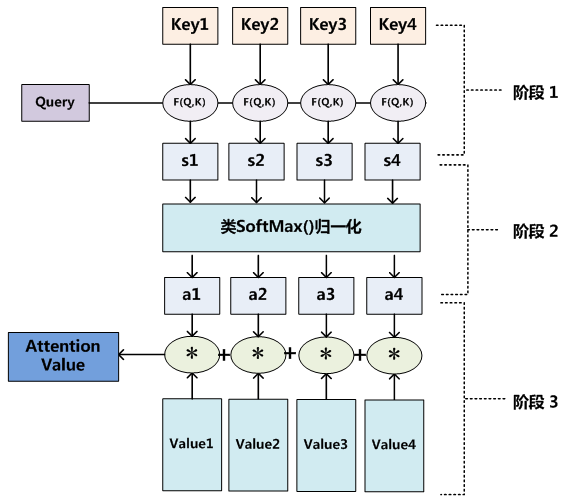
通过上图，Attention 通常可以进行如下描述，表示为将 Query(Q) 和 key-value pairs（把 Values 拆分成了键值对的形式）映射到输出上，其中 query、每个 key、每个 value 都是向量，输出是 V 中所有 values 的加权，其中权重是由 Query 和每个 key 计算出来的。

图中，K和V一般来说相等，在Transformer中K和V可以不相等，但是K和V之间一定具有某种联系，这样QK点乘之后才能指导V哪些重要，哪些不重要。

计算方法分为三步：

第一步：计算比较 $Q$ 和 $K$ 的相似度，用 $f$ 来表示($f(Q,K_i),i=1,2,3…m$)。一般第一步计算方法包括四种:
1、点乘（Transformer使用）：$f(Q,K_i)=Q^TK_i$
2、权重
3、拼接权重
4、感知机

第二步：将得到的相似度进行softmax操作，进行归一化：$a_i=softmax(\frac{f(Q,K_i)}{\sqrt{d_k}})$

除以 $\sqrt{d_k}$的作用：假设 $Q, K$里的元素的均值为0，方差为 1，那么$A^T=Q^TK$中元素的均值为0，方差为d。当d变得很大时，A中的元素方差也会很大，如果A中的元素方差很大，在数量级较大时，softmax将几乎全部的概率分布都分配给了最大值对应的标签，由于某一维度的数量级较大，进而会导致softmax未来求梯度时会消失。总的来说就是softmax(A)的分布会和d有关，因此A中每一个元素乘上$1/\sqrt{d_k}$后，方差又变为1，并且A的数量级也将会变小。

第三步：针对计算出来的权重$a_i$，对V中的所有values进行加权求和计算，得到Attention向量。Attention = $\sum_{i=1}^ma_iV_i$

Self-Attention

self-Attention机制如下图所示：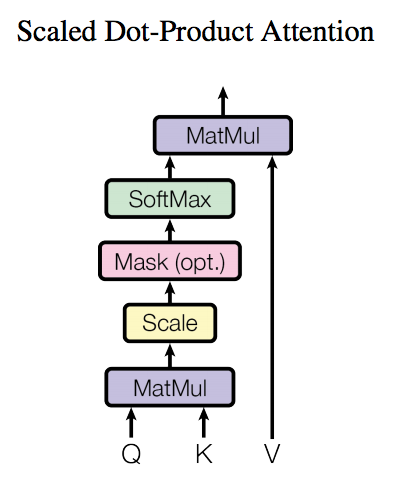

其与Attention机制除了QKV来源不同外，其余完全一致。

计算的公式如下：
$$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$

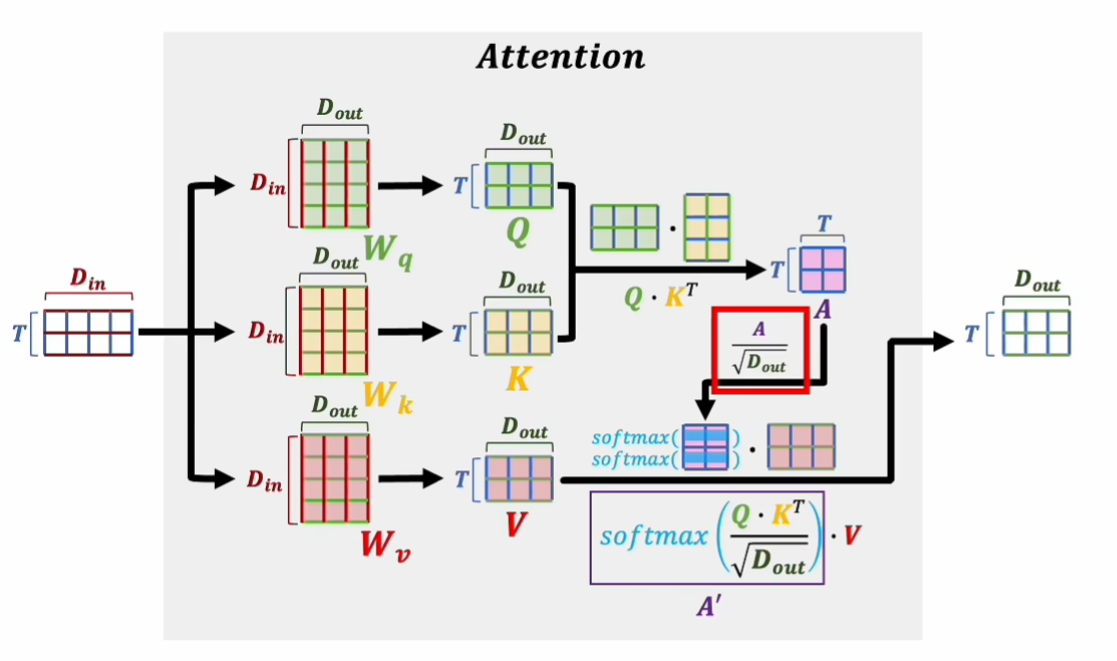
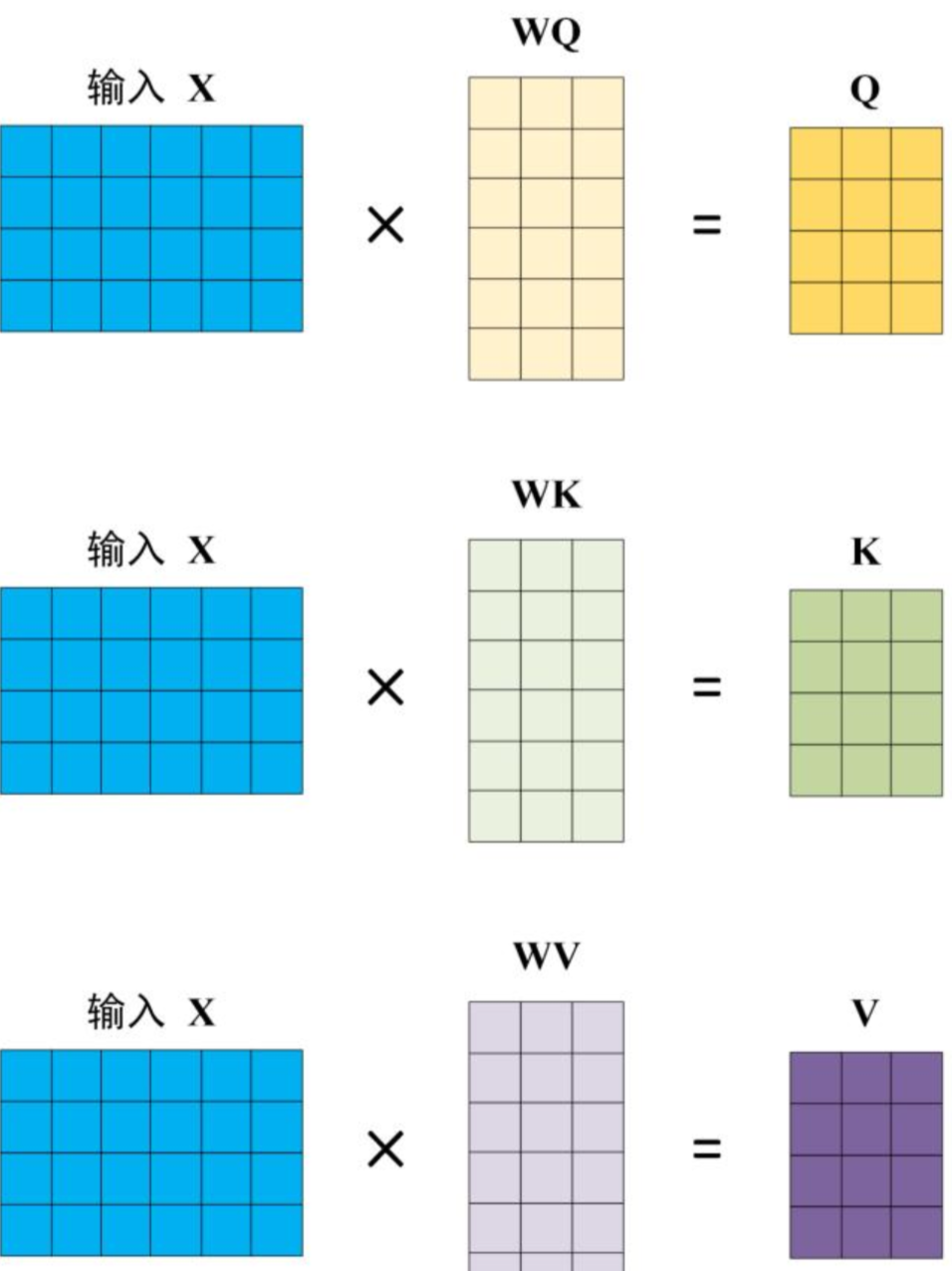
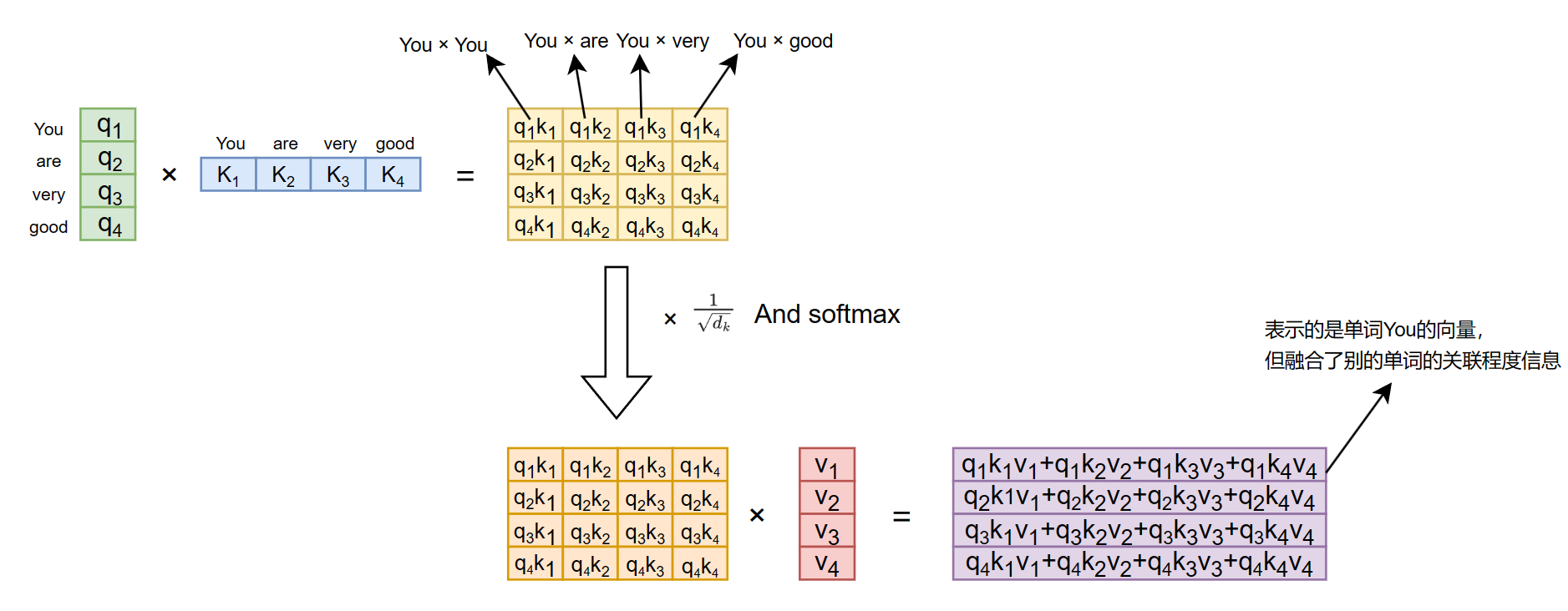
对于Q、K、V，其都来源于同一输入矩阵X。矩阵X经过不同的线性变阵矩阵$W_Q、W_K、W_V$计算从而得到$Q、K、V$

计算如下图所示，注意 $X、Q、K、V$ 的每一行都表示一个单词。

经过$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$计算，所得的值每一个行向量代表原来的单词向量，但是其融合了单词本身与句子中其他单词的关联性。

一个例子如下：

Attention和Self-Attention的区别：

Attention一个很宽泛（宏大）的一个概念，QKV 相乘就是注意力，但其没有规定QKV三个值是怎么来的。抽象理解就是通过一个查询变量 Q，去找到 V 里面与其相关联的信息。
一般，Q 可以是任意值，V 也是任意值， K往往是等同于V 的（或同源）。然后 QK 相乘求相似度A， AV 相乘得到注意力值Z。Z 就是 V 的另外一种形式的表示。
Self-Attention是一个相对狭隘的概念，其属于注意力机制。自注意力机制指定QKV同源，都来自于同一X，本质上 QKV 可以看做是相等的。

Masked Self-Attention

Masked Self-Attention基于Self-Attention，这里的 Masked 就是要在做语言模型（或者像翻译）的时候，不给模型看到未来的信息，它的结构如下图所示：

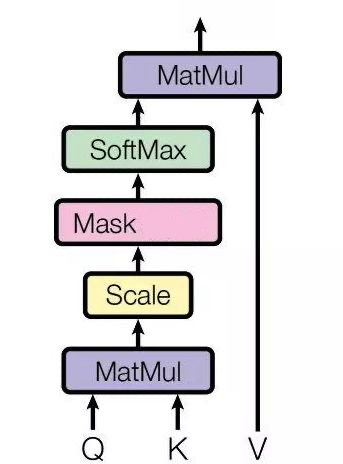
假设在此之前我们已经通过 scale 之前的步骤得到了一个 attention map，而 mask 就是沿着对角线把灰色的区域用0覆盖掉，不给模型看到未来的信息，如下图所示：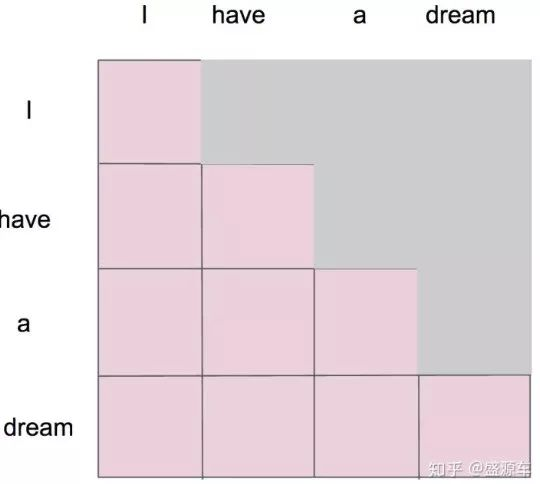

详细来说：
1、”i” 作为第一个单词，只能有和 “i” 自己的 attention；
2、”have” 作为第二个单词，有和 “i、have” 前面两个单词的 attention；
3、”a” 作为第三个单词，有和 “i、have、a” 前面三个单词的 attention；
4、”dream” 作为最后一个单词，才有对整个句子 4 个单词的 attention。

并且在做完 softmax 之后，横轴结果合为 1。如下图所示：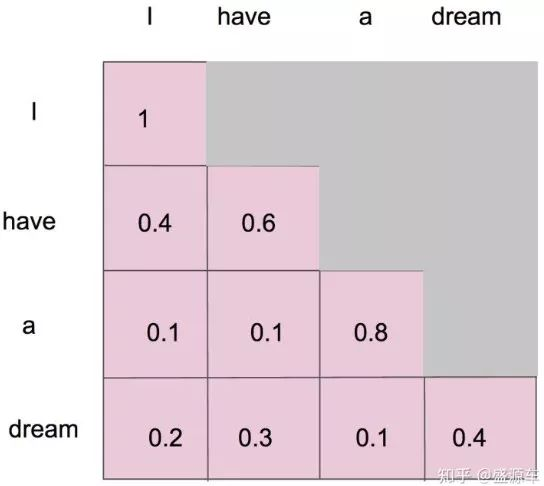

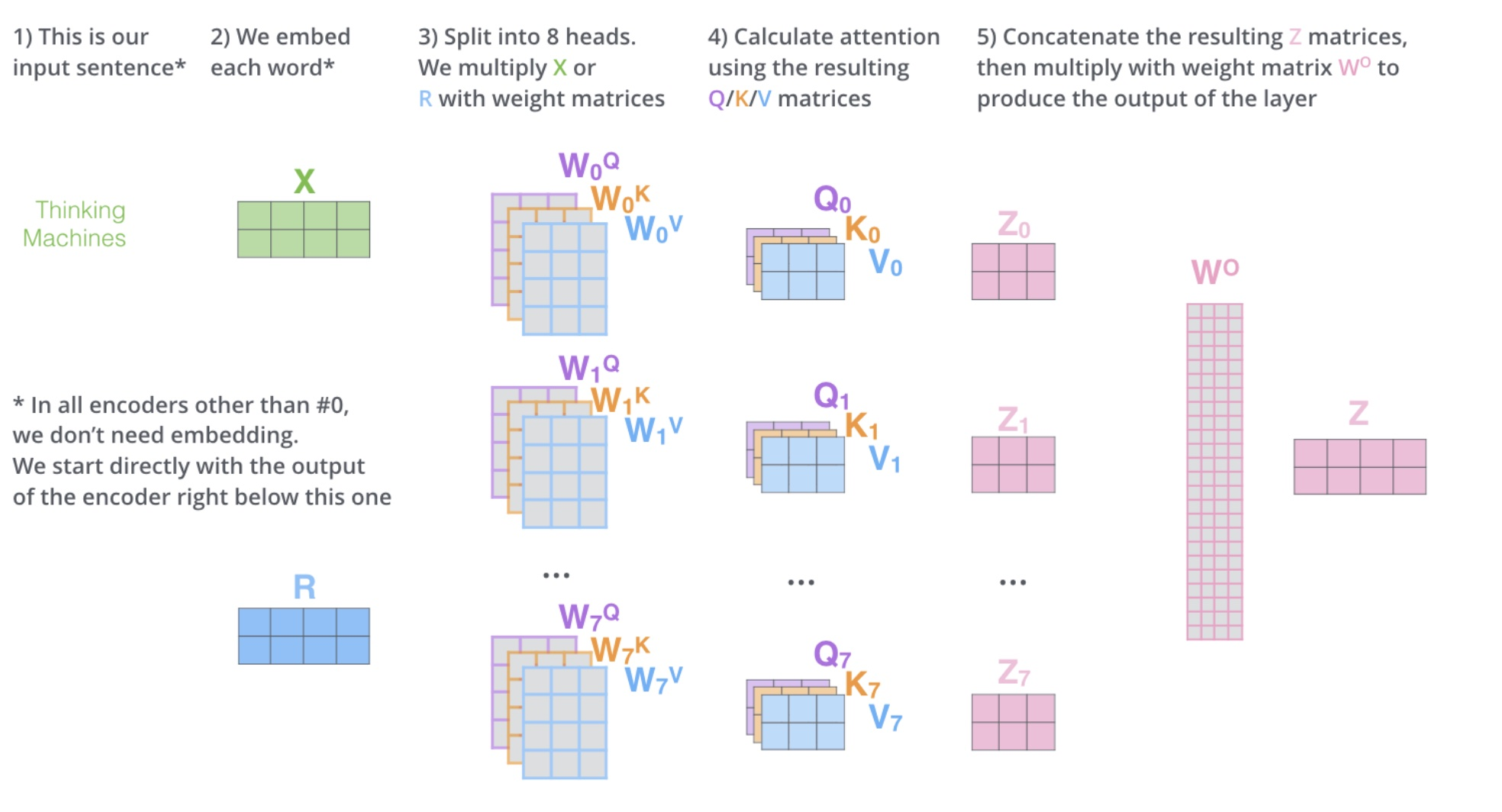
Mult-Head Self-Attention

Multi-Head Attention 是由多个 Self-Attention 组合形成的，下图是论文中 Multi-Head Attention 的结构图。

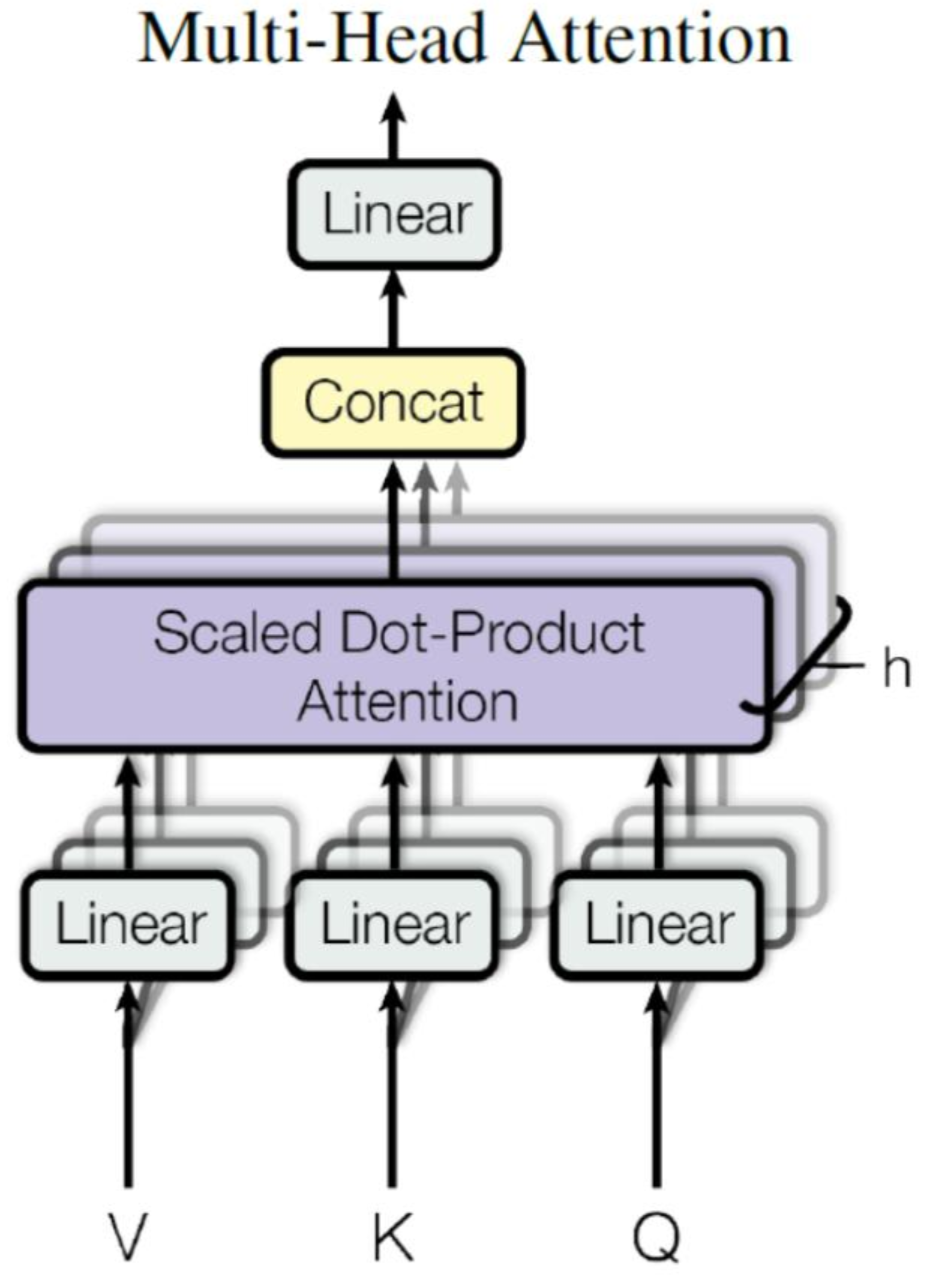
Multi-Head Attention 包含多个 Self-Attention 层，首先将输入$X$分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵$Z_i$，得到h个输出矩阵 $Z_1$到 $Z_h$之后，Multi-Head Attention 将它们拼接在一起 (Concat)，然后传入一个Linear层，得到 Multi-Head Attention 最终的输出$Z’$。

上述操作有什么好处呢？

多头相当于把原始信息 Source 放入了多个子空间中，也就是捕捉了多个信息，对于使用 multi-head attention 的简单回答就是，多头保证了 attention 可以注意到不同子空间的信息，捕捉到更加丰富的特征信息。其实本质上是论文原作者发现这样效果确实好。

Positional Encoding

我们已经知道，Self-Attention 的 $Q、K、V$ 三个矩阵是由同一个输入$X_1=(x_1,x_2,…,x_n)$线性转换而来，也就是说对于这样的一个被打乱序列顺序的 $X_2=(x_2,x_1,…,x_n)$而言，由于 Attention 值的计算最终会被加权求和，也就是说两者最终计算的 Attention 值都是一样的，进而也就表明了 Attention 丢掉了X的序列顺序信息。

为了解决 Attention 丢失的序列顺序信息，Transformer 的提出者提出了 Position Embedding，也就是对于输入 X 进行 Attention 计算之前，在 X 的词向量中加上位置信息。也就是说 X 的词向量为
$$X_{final_enbeding}=Embedding+Positional\ Encoding$$

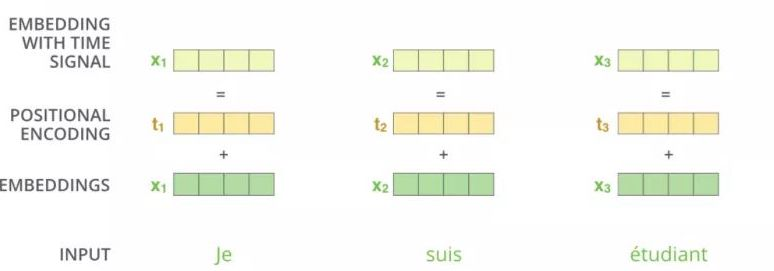
其中位置编码公式为：
$$
PE_{(pos,2i)} = sin(pos/10000^{2i/d})、PE_{(pos,2i+1)} = cos(pos/10000^{2i/d})
$$

其中，$pos$ 表示单词在句子中的位置，$d$ 表示 PE的维度 (与Word Embedding 一样)，$2i$ 表示偶数的维度，$2i+1$ 表示奇数维度 (即 $2i≤d, 2i+1≤d$)。

Position Embedding 本身是一个绝对位置的信息，但在语言模型中，相对位置也很重要。那么为什么位置嵌入机制有用呢？

原因如下：

由此可见，对于pos+k位置的位置向量某一维2i或2i+1而言，可以表示为pos位置与k位置的位置向量的2i维与2i+1维的线性组合，这样的线性组合意味着位置向量中蕴含了相对位置信息。

Transformer

Transformer整体结构如下：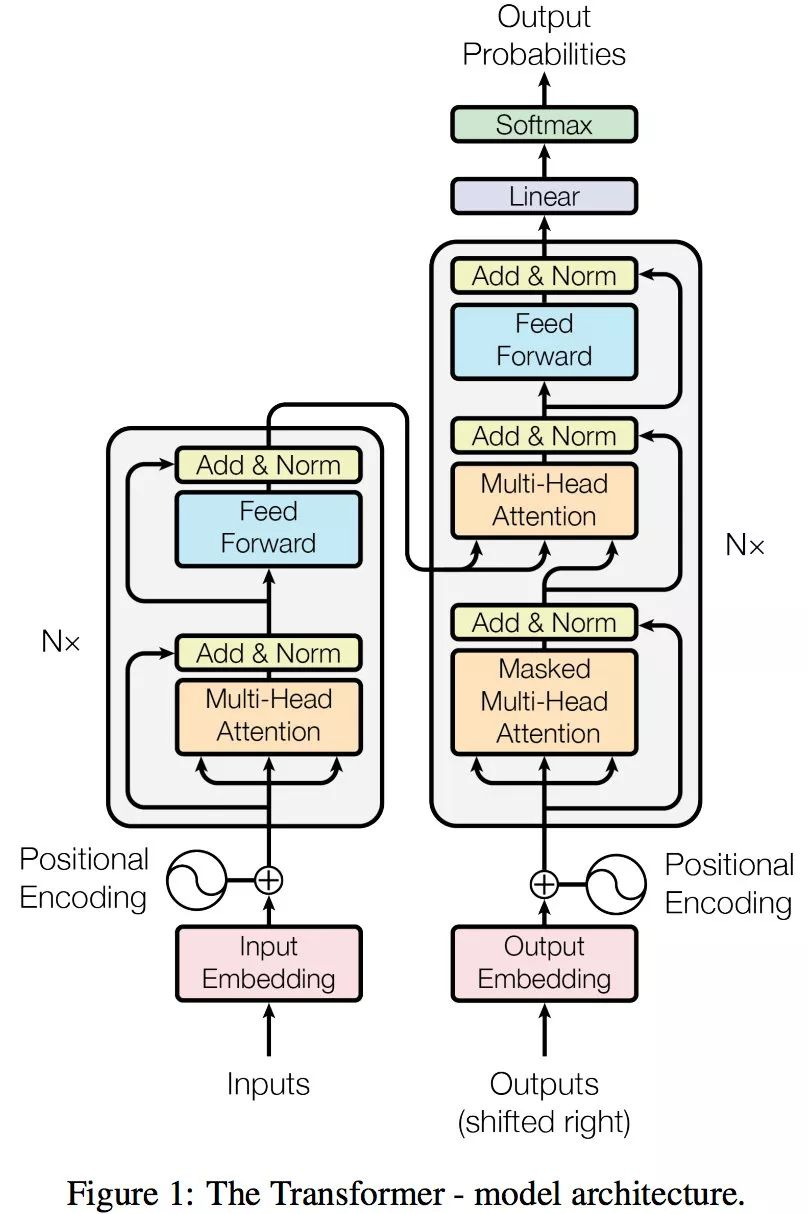

Transformer由编码器和解码器两部分组成，以一个翻译任务来说，编码器负责把输入变成一个词向量，解码器得到编码器输出的词向量后，生成翻译的结果。

“Nx” 的意思是，编码器里面又有 N 个小编码器（默认 N=6），通过 6 个编码器，对词向量一步又一步的强化（增强）。

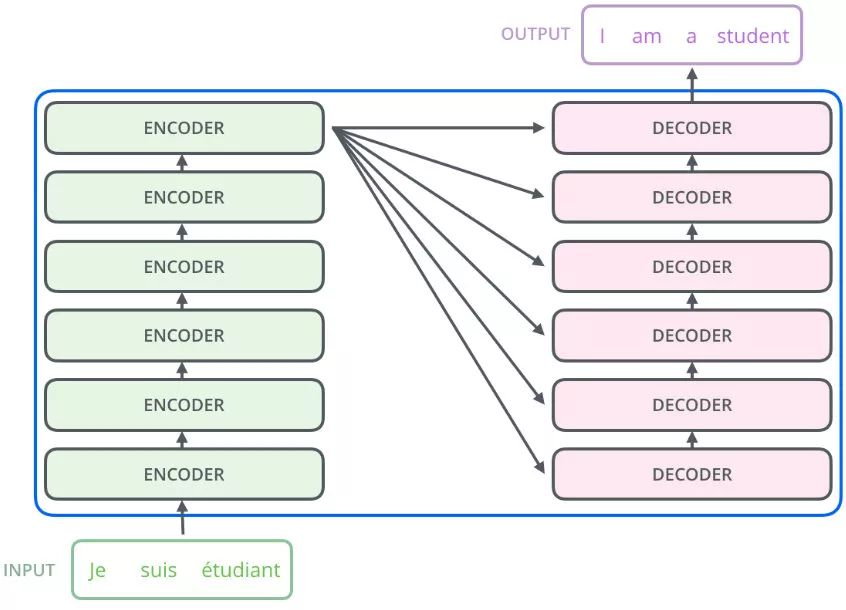
编码器Encoder

编码层包括两个子层：Self-Attention和Feed Forward。

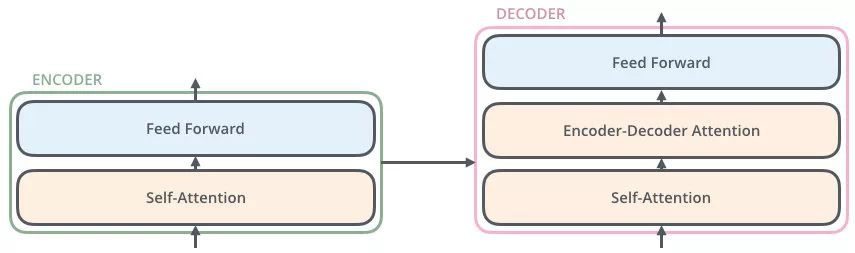
第一个 sub-layer 是 multi-head self-attention，用来计算输入的 self-attention；
第二个 sub-layer 是简单的前馈神经网络层 Feed Forward；

Encoder 的数据流示意图如下：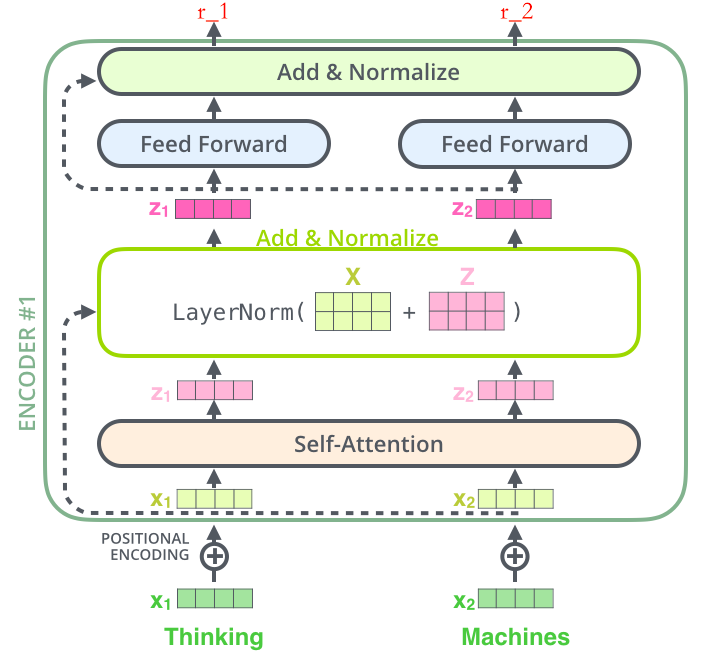

第一步、深绿色的 $x_1$表示 Embedding 层的输出，加上代表 Positional Embedding 的向量之后，得到最后输入 Encoder 中的特征向量，也就是浅绿色向量 $x_1$；

第二步、浅绿色向量 $x_1$表示单词 “Thinking” 的特征向量，其中 $x_1$ 经过 Self-Attention 层，变成浅粉色向量 $z_1$。

第三步、$x_1$作为残差结构的直连向量，直接和$z_1$相加，之后进行 Layer Norm 操作，得到深粉色向量$z_1$。

Add & Norm：Add & Norm 层由 Add 和 Norm 两部分组成。

Add指 $X+MultiHeadAttention(X)$，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，并且避免出现梯度消失的情况

Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以保证数据特征分布的稳定性，并且可以加速模型的收敛

第四步、$z_1$经过前馈神经网络（Feed Forward）层，经过残差结构与自身相加，之后经过 LN 层，得到一个输出向量 $r_1$

该前馈神经网络包括两个线性变换和一个ReLU激活函数。$Relu(w_2(w_1x+b_1)+b2)$

之后，$r_1$ 将会作为下一层 Encoder 的输入，代替 $x_1$ 的角色，如此循环，直至最后一层 Encoder。

总的来说，Encoder所做的一切事情都是为了产生词向量，只不过这个词向量更加优秀，让这个词向量能够更加精准。

解码器Decoder

解码器会接收编码器生成的词向量，然后通过这个词向量去生成翻译的结果。

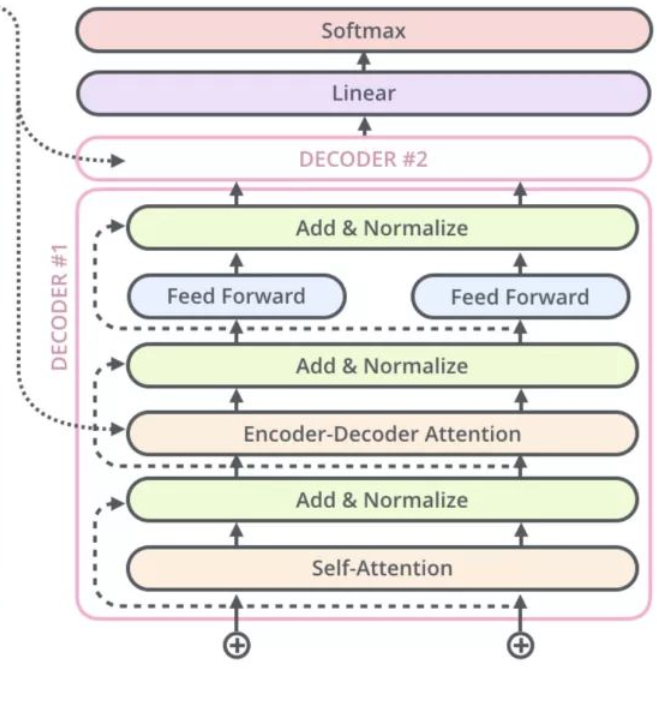
解码器分成三个子层：
第一个子层masked multi-head attention；
第二个子层是multi-head attention；
第三个子层是Feed Forward；

在decoder运行阶段，第一个子层的输入为已经生成的词，其经过Positional Encoding后进入Masked Multi-Head Attention，之后经过残差和归一化（Add&Norm）之后作为Q，Encoder的输出作为K、V，传入Multi-Haed Attention中，之后经过一个Feed Forward、Add&Norm 进入下一个Decoder。

为什么 Decoder 需要做 Mask？

在训练阶段：我们知道 “我是一个学生”的翻译结果为“I am a student”，我们把 “I am a student” 的 Embedding 输入到 Decoders 里面，翻译第一个词 “I” 时，

如果对 “I am a student” attention 计算不做 mask，“am，a，student” 对 “I” 的翻译将会有一定的贡献
如果对 “I am a student” attention 计算做 mask，“am，a，student” 对 “I” 的翻译将没有贡献

在测试阶段：我们不知道 “我爱中国” 的翻译结果为 “I love China”，我们只能随机初始化一个 Embedding 输入到 Decoders 里面，

翻译第一个词 “I” 时，无论是否做 mask，“love，China” 对 “I” 的翻译都不会产生贡献
但是翻译了第一个词 “I” 后，随机初始化的 Embedding 有了 “I” 的 Embedding，也就是说在翻译第二词 “love” 的时候，“I” 的 Embedding 将有一定的贡献，但是 “China” 对 “love” 的翻译毫无贡献，随之翻译的进行，已经翻译的结果将会对下一个要翻译的词都会有一定的贡献，这就和做了 mask 的训练阶段做到了一种匹配。

总结下就是：Decoder 做 Mask，是为了让训练阶段和测试阶段行为一致，不会出现间隙，避免过拟合

为什么 Encoder 给予 Decoders 的是 K、V 矩阵？

在Attention中，Query 的目的是借助它从一堆信息中找到重要的信息。

Q来源解码器，K=V来源于编码器。Q是查询变量，是已经生成的词，K=V 是源语句。

当我们生成这个词的时候，通过已经生成的词和源语句做自注意力，就是确定源语句中哪些词对接下来的词的生成更有作用。因此需要使用已经生成的词作为Q，到源语句中去查询与其相关联的信息，所以Encoder 传给Decoder的矩阵做的是 K和V。