逻辑回归（Logistic Regression）是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。

以二分类为例，对于所给数据集，假设存在这样的一条直线可以将数据完成线性可分。

Sigmoid函数
逻辑回归使用Sigmoid函数（也称为Logistic函数）将线性组合的输入映射到一个介于0和1之间的概率值。

sigmoid函数如下：
$$g(z) = \frac{1}{1+e^{-z}}$$

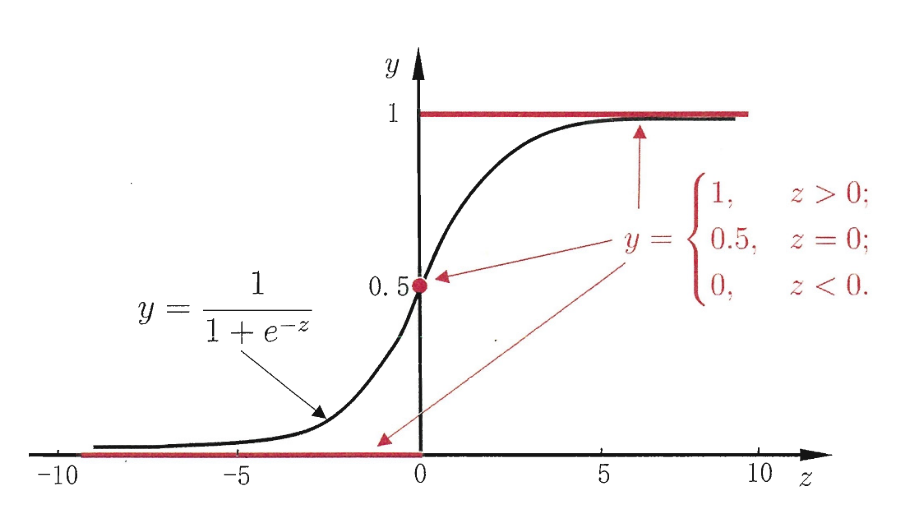
sigmoid函数易求导，适合梯度下降更新。其求导过程为：
$$g’(z) = (\frac{1}{1+e^{-z}})’ \ = \frac{e^{-z}}{(1+e^{-z})^2} ] \ = \frac{1}{1+e^{-z}} \frac{e^{-z}}{1+e^{-z}} = g(z)(1-g(z))$$

假设函数

逻辑回归假设函数的表达式为：
$$h_θ(x) = \frac{1}{1+e^{-θ^{T}x}}$$

其中，$h_\theta(x)$是预测的概率，$\theta$是模型的参数，$x$是输入特征。

对于二分类，其模型满足如下条件：
$$p(y=1|x;θ) = h(x)，p(y=0|x,θ) = 1-h(x)$$

其将逻辑回归的预测值赋予概率的意义。例如，$h(x)$是逻辑回归假设的目标函数，其值被定义于$y=1$（预测值为真）的概率。

上述两个式子可以合并为：
$$p(y|x;θ) = (h(x))^y(1-h(x))^{1-y}$$

损失函数：

似然函数：

$$L(θ) = \prod_{i = 1}^{m}P(y_i|x_i;θ) = \prod_{i = 1}^{m}(h_θ(x_i))^{y_i}(1-h_θ(x_i))^{1-{y_i}}$$

对数似然：
$$l(θ) = logL(θ) = \sum_{i=1}^{m}(y_{i}log(h_θ(x_i))+(1-y_i)log(1-h_θ(x_i)))$$

应用梯度上升求最大值，引入$J(θ) = -\frac{1}{m}l(θ)$，转换成梯度下降任务。

即对于二分类问题，损失函数的表达式为：
$$J(θ) = -\frac{1}{m}\sum_{i=1}^{m}[y_i\log(h_θ(x_i)) + (1 - y_i)\log(1 - h_θ(x_i))]$$

其中，$m$是训练样本的数量，$y_i$是样本的实际类别。

其对$θ$求偏导：
$$
\frac{\partial }{\partial θ}J(θ) = \frac{1}{m}\sum{i=1}^{m}(h_θ(x_i)-y_i)x_i
$$

参数更新：
$$θ_j := θ_j - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_θ(x_i)-y_i)x_i$$