Dar1in9's Blog HomeTagsCategoriesArchivesAbout
tensorflow
|机器学习
字数总计: 7.9k|阅读时长: 30 分钟

TensorFlow 是由 Google 开发的一个开源深度学习框架，专为大规模机器学习任务而设计，提供灵活的工具来构建和训练各类机器学习模型，尤其是神经网络。它支持从简单的模型构建到复杂的分布式训练，广泛应用于学术研究和工业生产中。

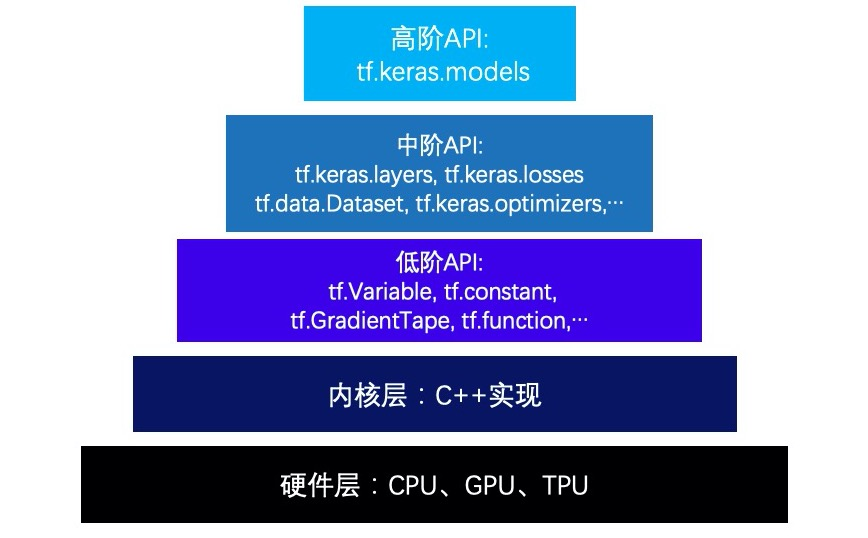
层次结构

TensorFlow的层次结构从低到高可以分成如下五层：硬件层，内核层，低阶API，中阶API，高阶API。

  • 第一层：硬件层，TensorFlow支持CPU、GPU或TPU加入计算资源池。
  • 第二层：内核层，为C++实现的内核，kernel可以跨平台分布运行。
  • 第三层：低阶API，由Python实现的操作符，提供了封装C++内核的低级API指令。主要包括各种张量操作算子、计算图、自动微分。
    如tf.Variable，tf.constant，tf.function，tf.GradientTape，tf.nn.softmax…
  • 第四层：中阶API，由Python实现的模型组件，对低级API进行了函数封装。主要包括数据管道(tf.data)、特征列(tf.feature_column)、激活函数(tf.nn)、模型层(tf.keras.layers)、损失函数(tf.keras.losses)、评估函数(tf.keras.metrics)、优化器(tf.keras.optimizers)、回调函数(tf.keras.callbacks) 等等。
  • 第五层：高阶API，由Python实现的模型成品。主要为tf.keras.models提供的模型的类接口，主要包括：模型的构建（Sequential、functional API、Model子类化）、型的训练（内置fit方法、内置train_on_batch方法、自定义训练循环、单GPU训练模型、多GPU训练模型、TPU训练模型）、模型的部署（tensorflow serving部署模型、使用spark(scala)调用tensorflow模型）。

低阶API

TensorFlow的低阶API主要包括张量操作，计算图和自动微分。

如果把模型比作一个房子，那么低阶API就是【模型之砖】。在低阶API层次上，可以把TensorFlow当做一个增强版的numpy来使用。TensorFlow提供的方法比numpy更全面，运算速度更快，如果需要的话，还可以使用GPU进行加速。

张量

TensorFlow的基本数据结构是张量（Tensor），即多维数组。按照行为特性进行划分，TensorFlow中有两种类型的张量——常量和变量。

其中常量是数值不能改变的张量，一般使用constant()函数进行创建：

1
2
# 创建一个常量x
x = tf.constant(10)

不同类型的数据可以使用不同维度的张量来表示。标量为0维张量；向量为1维张量；矩阵为2维张量；彩色图像有RGB三个通道，可以表示为3维度张量；视频在彩色图像的基础上增加时间维度，可以表示为4维张量等等。

通过传入嵌套列表的形式，可以利用constant()函数生成多维张量：

1
2
3
4
5
6
7
8
9
# 向量:1维张量
vector = tf.constant([1.0, 2.0, 3.0, 4.0]) 
# <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1., 2., 3., 4.], dtype=float32)>

# 矩阵:2维张量
matrix = tf.constant([[1.0, 2.0], [3.0, 4.0]])
# <tf.Tensor: shape=(2, 2), dtype=float32, numpy=
# array([[1., 2.],
#        [3., 4.]], dtype=float32)

模型中需要被训练的参数一般设置为变量,可利用Variable()函数将变量标记为“可训练”的，被标记了的变量会在反向传播中记录自己的梯度信息，并且变量的值可以用assign(), assign_add(), assign_sub()等方法给变量重新赋值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 张量赋值：assgin(value)将张量赋值为新的张量value
v = tf.Variable([1.0, 1.0])
v.assign([1.0, 2.0])
tf.print(v)    # 将张量的内容输出
# [1., 2.]

# 张量相加：assign_add(value)在原张量上相加，相当于 v = v + value
v.assign_add([1.0, 1.0])
tf.print(v)
# [2., 3.]

# 张量相减：assign_sub(value)在原张量上相减，相当于 v = v - value
v.assign_sub([1.0, 1.0])
tf.print(v)
# [1., 2.]

张量的操作主要包括张量的结构操作与数学运算。

  • 张量结构操作诸如：张量创建、索引切片、维度变换、合并分割；
  • 张量数学运算主要有：标量运算、向量运算、矩阵运算。

张量的结构操作

张量创建
除了constant()方法外，还有其他特殊张量的创建方法，张量创建的许多方法和numpy中创建array的方法类似。

1
2
3
4
tf.range(start,limit,delta)    # 创建从start到limit步长为delta的一维张量

b = tf.range(1, 10, delta=2)
# [1 3 5 7 9]

很多时候数据是由 numpy 格式给出，可以通过tf.convert_to_tensor(数据名，dtype=数据类型) 函数将numpy格式化为Tensor格式。同时也可以使用.numpy()方法将张量转变为numpy格式。

1
2
3
4
5
6
7
8
import numpy as np

a = np.arange(0, 5)
# 将numpy格式数据变量a转换成Tensor格式
b = tf.convert_to_tensor(a, dtype=tf.int64 )

# 将Tensor格式转换成numpy格式数据
c = b.numpy()

可采用不同函数创建不同类型的“矩阵形”张量，如tf.zeros(shape)创建全为0的张量，tf.fill(dims, value)创建全为指定值的张量。

1
2
3
4
5
6
7
d = tf.zeros([2,3])
# [[0 0 0]
#  [0 0 0]]

b = tf.fill([2,3], 5)
# [[5 5 5]
#  [5 5 5]]

更多类似的常用函数：

1
2
3
4
5
6
7
8
9
10
11
ones(shape, dtype)	# 创建指定维度的全1矩阵
# tf.ones(shape=[2,3]，dtype= tf.float32)	创建维度为(2,3),float32数据类型的全1矩阵

eye(num_rows, num_columns)	# 创建指定维度的单位矩阵
# tf.eye(num_rows=3, num_columns=3)	创建维度为(3,3)的单位矩阵

linalg.diag(diagonal, dtype)	# 创建指定对角元素的对角阵
# tf.linalg.diag(diagonal=[1,2])	创建对角元素为(1,2)的对角阵

zeros_like(input, dtype)	# 创建与指定张量相同维度的全0张量
# tf.zeros_like(input=[2,3])	创建与张量[2,3]同维度的全0张量

可创建服从各类分布的张量：

1
2
tf.random.uniform([5], minval=0, maxval=10)     # 均匀分布随机
tf.random.normal([3, 3], mean=0.0, stddev=1.0)  # 正态分布随机

索引切片

张量的索引切片方式和numpy中切分类似，切片时支持缺省参数和省略号。

可以使用tf.slice(input, begin, size)从指定起始位置处，提取指定切片大小的连续子区域。
对于不规则的切片提取，可以用tf.gather(params, indices, validate_indices=None, axis=None)，提取指定张量索引的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 生成区间0到10的维度为(5,5)均匀分布随机数张量
t=tf.random.uniform([3,5],minval=0, maxval=10, dtype=tf.int32)
# array([[4, 1, 6, 9, 3],
#        [6, 3, 5, 1, 7],
#        [1, 2, 9, 9, 1]])>

# 提取第1、2行
tf.print(t[1:])
# array([[6, 3, 5, 1, 7],
#       [1, 2, 9, 9, 1]])>

# 从张量[2,0]处起始，提取[2,3]大小的连续子区域张量
tf.slice(t, [1,0],[2,3])
# array([[6, 3, 5],
#        [1, 2, 9]])>

# 抽取第0、4列
p = tf.gather(t, [0, 4], axis=1)
# array([[4, 3],
#        [6, 7],
#        [1, 1]])>

若要通过修改张量的部分元素值得到新的张量，可以使用tf.where函数。tf.where可以理解为if的张量版本，此外还可以用于查询满足条件的元素的位置坐标。

1
2
3
4
5
6
7
8
9
# 如果tf.where只有一个参数，将返回所有满足条件的位置坐标
tf.where([True, False, False, True])
# <tf.Tensor: shape=(2, 1), dtype=int64, numpy=
# array([[0],
#        [3]])>

#tf.where如果包含三个参数，可以理解为if的张量版本
tf.where([True, False, False, True], [1,2,3,4], [100])
# <tf.Tensor: shape=(4,), dtype=int32, numpy=array([  1, 100, 100,   4], dtype=int32)>

维度变换

tf.reshape(tensor, shape) 改变张量的形状
tf.squeeze(input, axis=None) 减少维度
tf.expand_dims(input, axis) 增加维度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
a = tf.linspace(1, 20, 20)
# array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12., 13.,
#        14., 15., 16., 17., 18., 19., 20.])>

# 将张量a改成[4,5]形状的张量
b = tf.reshape(a, (1, 4, 5))
# <tf.Tensor: shape=(1, 4, 5), dtype=float64, numpy=
# array([[[ 1.,  2.,  3.,  4.,  5.],
#         [ 6.,  7.,  8.,  9., 10.],
#         [11., 12., 13., 14., 15.],
#         [16., 17., 18., 19., 20.]]])>


# 消除张量a中只有一个元素的维度
c = tf.squeeze(b)
# <tf.Tensor: shape=(4, 5), dtype=float64, numpy=
# array([[ 1.,  2.,  3.,  4.,  5.],
#        [ 6.,  7.,  8.,  9., 10.],
#        [11., 12., 13., 14., 15.],
#        [16., 17., 18., 19., 20.]])>


# 在第0维插入长度为1的一个维度
d = tf.expand_dims(c, axis=0)  
# <tf.Tensor: shape=(1, 4, 5), dtype=float64, numpy=
# array([[[ 1.,  2.,  3.,  4.,  5.],
#         [ 6.,  7.,  8.,  9., 10.],
#         [11., 12., 13., 14., 15.],
#         [16., 17., 18., 19., 20.]]])>

合并分割
与numpy类似，张量可以用tf.concat和tf.stack方法进行合并，其中tf.concat是连接，不会增加维度，而tf.stack是堆叠，会增加维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 将张量a、b合并，维度不增加
a = tf.constant([[1,2],[3,4]])
b = tf.constant([[5,6],[7,8]])
tf.concat([a,b], axis=1)
# <tf.Tensor: shape=(2, 4), dtype=int32, numpy=
# array([[1, 2, 5, 6],
#        [3, 4, 7, 8]], dtype=int32)>

# 将张量a、b堆叠，维度增加
tf.stack([a,b])
# <tf.Tensor: shape=(2, 2, 2), dtype=int32, numpy=
# array([[[1, 2],
#         [3, 4]],
#        [[5, 6],
#         [7, 8]]], dtype=int32)>

张量的数学操作

标量运算

张量的四则运算、三角函数、指数、对数、余数、逻辑运算都是标量运算符。

标量运算符的特点是对张量实施逐元素运算，有些标量运算符对常用的数学运算符进行了重载，并支持类似numpy的广播特性，需要注意的是张量的四则运算必修满足相同维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
a = tf.constant([[1,2],[-3,4]])
b = tf.constant([[5,6],[7,8]])

#对应元素相加
tf.print(a+b)
# [[6 8]
#  [4 12]]

#对应元素相乘
tf.print(a*b)
# [[5 12]
#  [-21 32]]

#逻辑运算
print(a>0)
# tf.Tensor(
# [[ True  True]
#  [False  True]], shape=(2, 2), dtype=bool)

向量运算

向量运算符只在一个特定轴上运算，将一个向量映射到一个标量或者另外一个向量。

许多向量运算符都以reduce开头，可用tf.reduce_mean(input_tensor, axis=None)计算张量沿着指定维度的平均值。
可用tf.reduce_min，tf.reduce_max 计算张量维度上元素的最小、最大值，tf.reduce_sum对张量求和，用tf.argmax，tf.argmin求张量维度上最大最小值的索引。

axis代表变动的操作轴

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
x=tf.constant([[1,2,3],[4,5,6]])
tf.print(tf.reduce_mean(x, axis=0))    # 求列平均
# [2 3 4]
# axis=0，表示第0维变动，
# 从(0,0)、(1,0)获取第0个结果
# 从(0,1)、(1,1)获取第1个结果
# ...

tf.print(tf.reduce_sum(x,axis=0))     # 求列和
# [5 7 9]

tf.print(tf.reduce_max(x,axis=1))     # 求行最大值
# [3 6]

tf.print(tf.argmax(x,axis=1))         # 求行最大值索引
# [2 2]

矩阵运算

矩阵运算要求张量必须是二维的，包括矩阵乘法，矩阵转置，矩阵逆，矩阵求迹，矩阵行列式，矩阵求特征值等运算。

除了一些常用的运算外，大部分和矩阵有关的运算都在tf.linalg子包中。

1
2
3
4
5
6
7
8
a = tf.constant([[1,2],[3,4]])
b = tf.constant([[2,0],[0,2]])

# 矩阵乘法
tf.matmul(a,b) #等价于a@b
# <tf.Tensor: shape=(2, 2), dtype=int32, numpy=
# array([[2, 4],
#        [6, 8]])>
1
2
3
4
5
matmul(a,b)	    # 矩阵相乘
transpose(a)	# 矩阵转置
linalg.inv(a)	# 矩阵求逆
linalg.trace(a)	# 矩阵求集
linalg.det(a)	# 行列式求值

计算图

计算图是TensorFlow中最基本的一个概念，TensorFlow中所有的计算都会被转化为计算图上的节点，其中计算图有三种构建方式：静态计算图、动态计算图以及Autograph。

计算图由节点(nodes)和线(edges)组成。节点表示操作符Operator，或者称之为算子，线表示计算间的依赖。实线表示有数据传递依赖，传递的数据即张量。虚线通常可以表示控制依赖，即执行先后顺序。

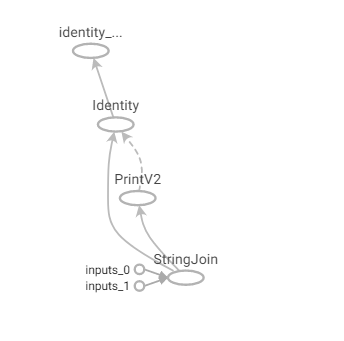
在TensorFlow1.0时代，采用的是静态计算图，需要先使用TensorFlow的各种算子创建计算图，然后再开启一个会话Session，显式执行计算图。
而在TensorFlow2.0时代，采用的是动态计算图，即每使用一个算子后，该算子会被动态加入到隐含的默认计算图中立即执行得到结果，而无需开启Session。

1
2
3
4
5
6
# 动态计算图连接字符串张量，动态计算图在每个算子处构建，构建后立即执行
x = tf.constant("hello")
y = tf.constant("world")
z = tf.strings.join([x,y], separator=" ")
tf.print(z)
# hello world

自动微分机制

梯度磁带

神经网络通常依赖反向传播求梯度来更新网络参数，求梯度过程通常是一件非常复杂而容易出错的事情，而深度学习框架可以帮助我们自动地完成这种求梯度运算。

Tensorflow一般使用梯度磁带tf.GradientTape函数来记录正向运算过程，然后反播磁带自动得到梯度值，这种利用tf.GradientTape求微分的方法叫做Tensorflow的自动微分机制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 求二阶导数，原函数形如f(x) = a*x**2 + b*x + c
x = tf.Variable(0.0, name="x", dtype=tf.float32)

a = tf.constant(1.0)
b = tf.constant(-2.0)
c = tf.constant(1.0)

# 定义两个梯度磁带求解二阶梯度
with tf.GradientTape() as tape2:
    with tf.GradientTape() as tape1: 
        # 最内层梯度磁带中声明目标函数（损失函数） 
        y = a*tf.pow(x, 2) + b*x + c
    # gradient方法对y求一阶导
    dy_dx = tape1.gradient(y,x)   
# gradient方法对一阶导dy_dx 再求导
dy2_dx2 = tape2.gradient(dy_dx,x)

print(dy2_dx2)
tf.Tensor(2.0, shape=(), dtype=float32)

中阶API

TensorFlow的中阶API主要包括:

数据管道(tf.data)、特征列(tf.feature_column)、激活函数(tf.nn)、模型层(tf.keras.layers)、损失函数(tf.keras.losses)、评估函数(tf.keras.metrics)、优化器(tf.keras.optimizers)、回调函数(tf.keras.callbacks)

如果把模型比作一个房子，那么中阶API就是【模型之墙】。

数据管道Dataset

如果需要训练的数据大小不大，例如不到1G，那么可以直接全部读入内存中进行训练，这样一般效率最高。但如果需要训练的数据很大，例如超过10G，无法一次载入内存，那么通常需要在训练的过程中分批逐渐读入。

使用 tf.data API 可以构建数据输入管道，轻松处理大量的数据，不同的数据格式，以及不同的数据转换。

可以从 Numpy array、Pandas DataFrame、Python generator、csv文件、文本文件、文件路径、tfrecords文件等方式构建数据管道。

从Numpy array构建数据管道

1
2
3
4
5
6
7
8
9
10
11
12
# 从Numpy array构建数据管道

import tensorflow as tf
import numpy as np 
from sklearn import datasets 


iris = datasets.load_iris()

ds1 = tf.data.Dataset.from_tensor_slices((iris["data"], iris["target"]))
for features,label in ds1.take(5):
    print(features,label)

从 Pandas DataFrame构建数据管道

1
2
3
4
5
6
7
8
9
10
11
12
13
# 从 Pandas DataFrame构建数据管道
import tensorflow as tf
from sklearn import datasets 
import pandas as pd


iris = datasets.load_iris()
dfiris = pd.DataFrame(iris["data"],columns = iris.feature_names)

ds2 = tf.data.Dataset.from_tensor_slices((dfiris.to_dict("list"),iris["target"]))

for features,label in ds2.take(3):
    print(features,label)

从csv文件构建数据管道

1
2
3
4
5
6
7
8
9
10
11
# 从csv文件构建数据管道
ds4 = tf.data.experimental.make_csv_dataset(
      file_pattern = ["../../data/titanic/train.csv","../../data/titanic/test.csv"],
      batch_size=3, 
      label_name="Survived",
      na_value="",
      num_epochs=1,
      ignore_errors=True)

for data,label in ds4.take(2):
    print(data,label)

特征列feature_column

特征列 通常用于对结构化数据实施特征工程时候使用，图像或者文本数据一般不会用到特征列。

激活函数activation

激活函数在深度学习中扮演着非常重要的角色，它给网络赋予了非线性，从而使得神经网络能够拟合任意复杂的函数。如果没有激活函数，无论多复杂的网络，都等价于单一的线性变换，无法对非线性函数进行拟合。

目前，深度学习中最流行的激活函数为 relu, 但也有些新推出的激活函数，例如 swish、GELU 据称效果优于relu激活函数。

常用激活函数

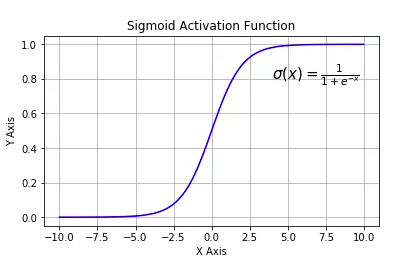
tf.nn.sigmoid：将实数压缩到0到1之间，一般只在二分类的最后输出层使用。主要缺陷为存在梯度消失问题，计算复杂度高，输出不以0为中心。

tf.nn.softmax：sigmoid的多分类扩展，一般只在多分类问题的最后输出层使用。

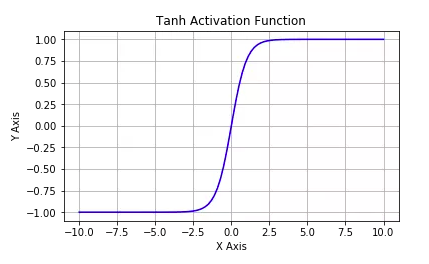
tf.nn.tanh：将实数压缩到-1到1之间，输出期望为0。主要缺陷为存在梯度消失问题，计算复杂度高。

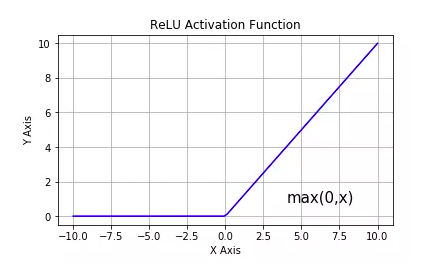
tf.nn.relu：修正线性单元，最流行的激活函数。一般隐藏层使用。主要缺陷是：输出不以0为中心，输入小于0时存在梯度消失问题(死亡relu)。

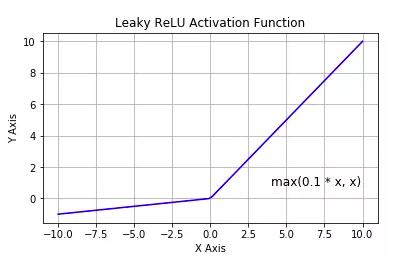
tf.nn.leaky_relu：对修正线性单元的改进，解决了死亡relu问题。

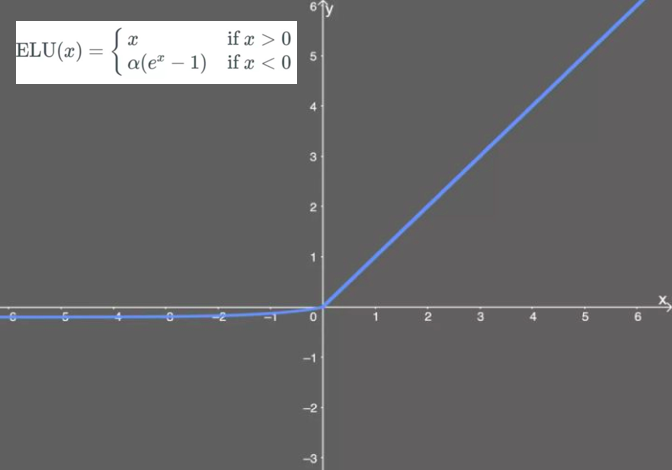
tf.nn.elu：指数线性单元。对relu的改进，能够缓解死亡relu问题。

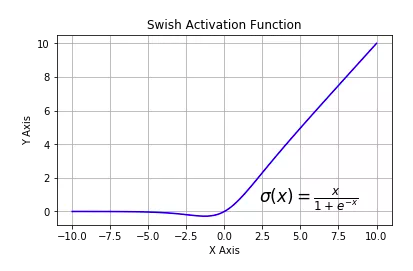
tf.nn.swish：自门控激活函数。谷歌出品，相关研究指出用swish替代relu将获得轻微效果提升。

在模型中使用激活函数

在keras模型中使用激活函数一般有两种方式，一种是作为某些层的activation参数指定，另一种是显式添加layers.Activation激活层。

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras import layers,models

tf.keras.backend.clear_session()

model = models.Sequential()
model.add(layers.Dense(32,input_shape = (None,16), activation = tf.nn.relu)) #通过activation参数指定
model.add(layers.Dense(10))
model.add(layers.Activation(tf.nn.softmax))  # 显式添加layers.Activation激活层
model.summary()

模型层layers

深度学习模型一般由各种模型层组合而成。

tf.keras.layers内置了非常丰富的各种功能的模型层。例如：
layers.Dense、layers.Flatten、layers.Input、layers.DenseFeature、layers.Dropout、layers.Conv2D、layers.MaxPooling2D、layers.Conv1D、layers.Embedding、layers.GRU、layers.LSTM、layers.Bidirectional等等。

如果这些内置模型层不能够满足需求，我们也可以通过编写tf.keras.Lambda匿名模型层或继承tf.keras.layers.Layer基类构建自定义的模型层。其中tf.keras.Lambda匿名模型层只适用于构造没有学习参数的模型层。

内置模型层
一些常用的内置模型层简单介绍如下。

基础层：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Dense            # 密集连接层。参数个数=输入层特征数×输出层特征数(weight)＋输出层特征数(bias)
Activation       # 激活函数层。一般放在Dense层后面，等价于在Dense层中指定activation。
Dropout          # 随机置零层。训练期间以一定几率将输入置0，一种正则化手段。
BatchNormalization    # 批标准化层。通过线性变换将输入批次缩放平移到稳定的均值和标准差。可以增强模型对输入不同分布的适应性，加快模型训练速度，有轻微正则化效果。一般在激活函数之前使用。
SpatialDropout2D    # 空间随机置零层。训练期间以一定几率将整个特征图置0，一种正则化手段，有利于避免特征图之间过高的相关性。
Input               # 输入层。通常使用Functional API方式构建模型时作为第一层。
DenseFeature        # 特征列接入层，用于接收一个特征列列表并产生一个密集连接层。
Flatten             # 压平层，用于将多维张量压成一维。
Reshape             # 形状重塑层，改变输入张量的形状。
Concatenate         # 拼接层，将多个张量在某个维度上拼接。
Add                 # 加法层。
Subtract            # 减法层。
Maximum             # 取最大值层。
Minimum             # 取最小值层。

卷积网络相关层

1
2
3
4
5
6
7
8
9
10
11
Conv1D    # 普通一维卷积，常用于文本。参数个数 = 输入通道数×卷积核尺寸(如3)×卷积核个数
Conv2D    # 普通二维卷积，常用于图像。参数个数 = 输入通道数×卷积核尺寸(如3乘3)×卷积核个数
Conv3D    # 普通三维卷积，常用于视频。参数个数 = 输入通道数×卷积核尺寸(如3乘3乘3)×卷积核个数
SeparableConv2D    # 二维深度可分离卷积层。不同于普通卷积同时对区域和通道操作，深度可分离卷积先操作区域，再操作通道。即先对每个通道做独立卷积操作区域，再用1乘1卷积跨通道组合操作通道。参数个数 = 输入通道数×卷积核尺寸 + 输入通道数×1×1×输出通道数。深度可分离卷积的参数数量一般远小于普通卷积，效果一般也更好。
DepthwiseConv2D    # 二维深度卷积层。仅有SeparableConv2D前半部分操作，即只操作区域，不操作通道，一般输出通道数和输入通道数相同，但也可以通过设置depth_multiplier让输出通道为输入通道的若干倍数。输出通道数 = 输入通道数 × depth_multiplier。参数个数 = 输入通道数×卷积核尺寸× depth_multiplier。
Conv2DTranspose    # 二维卷积转置层，俗称反卷积层。并非卷积的逆操作，但在卷积核相同的情况下，当其输入尺寸是卷积操作输出尺寸的情况下，卷积转置的输出尺寸恰好是卷积操作的输入尺寸。
LocallyConnected2D    # 二维局部连接层。类似Conv2D，唯一的差别是没有空间上的权值共享，所以其参数个数远高于二维卷积。
MaxPool2D             # 二维最大池化层。也称作下采样层。池化层无可训练参数，主要作用是降维。
AveragePooling2D      # 二维平均池化层。
GlobalMaxPool2D       # 全局最大池化层。每个通道仅保留一个值。一般从卷积层过渡到全连接层时使用，是Flatten的替代方案。
GlobalAvgPool2D       # 全局平均池化层。每个通道仅保留一个值。

循环网络相关层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Embedding        # 嵌入层。一种比Onehot更加有效的对离散特征进行编码的方法。一般用于将输入中的单词映射为稠密向量。嵌入层的参数需要学习。
LSTM             # 长短记忆循环网络层。最普遍使用的循环网络层。具有携带轨道，遗忘门，更新门，输出门。可以较为有效地缓解梯度消失问题，从而能够适用长期依赖问题。设置return_sequences = True时可以返回各个中间步骤输出，否则只返回最终输出。
GRU              # 门控循环网络层。LSTM的低配版，不具有携带轨道，参数数量少于LSTM，训练速度更快。
SimpleRNN        # 简单循环网络层。容易存在梯度消失，不能够适用长期依赖问题。一般较少使用。
ConvLSTM2D       # 卷积长短记忆循环网络层。结构上类似LSTM，但对输入的转换操作和对状态的转换操作都是卷积运算。
Bidirectional    # 双向循环网络包装器。可以将LSTM，GRU等层包装成双向循环网络。从而增强特征提取能力。
RNN：RNN基本层。接受一个循环网络单元或一个循环单元列表，通过调用tf.keras.backend.rnn函数在序列上进行迭代从而转换成循环网络层。
LSTMCell             # LSTM单元。和LSTM在整个序列上迭代相比，它仅在序列上迭代一步。可以简单理解LSTM即RNN基本层包裹LSTMCell。
GRUCell              # GRU单元。和GRU在整个序列上迭代相比，它仅在序列上迭代一步。
SimpleRNNCell        # SimpleRNN单元。和SimpleRNN在整个序列上迭代相比，它仅在序列上迭代一步。
AbstractRNNCell      # 抽象RNN单元。通过对它的子类化用户可以自定义RNN单元，再通过RNN基本层的包裹实现用户自定义循环网络层。
Attention            # Dot-product类型注意力机制层。可以用于构建注意力模型。
AdditiveAttention    # Additive类型注意力机制层。可以用于构建注意力模型。
TimeDistributed      # 时间分布包装器。包装后可以将Dense、Conv2D等作用到每一个时间片段上。

损失函数losses

一般来说，监督学习的目标函数由损失函数和正则化项组成。（Objective = Loss + Regularization）

对于keras模型，目标函数中的正则化项一般在各层中指定，例如使用Dense的 kernel_regularizer和 bias_regularizer等参数指定权重使用l1或者l2正则化项，此外还可以用kernel_constraint 和 bias_constraint等参数约束权重的取值范围，这也是一种正则化手段。

损失函数在模型编译时候指定。

  • 对于回归模型，通常使用的损失函数是均方损失函数 mean_squared_error。
  • 对于二分类模型，通常使用的是二元交叉熵损失函数 binary_crossentropy。
  • 对于多分类模型，如果label是one-hot编码的，则使用类别交叉熵损失函数 categorical_crossentropy。如果label是类别序号编码的，则需要使用稀疏类别交叉熵损失函数 sparse_categorical_crossentropy。
1
2
3
4
5
6
7
8
9
10
11
12
tf.keras.backend.clear_session()

model = models.Sequential()
model.add(layers.Dense(64, input_dim=64,
                kernel_regularizer=regularizers.l2(0.01), 
                activity_regularizer=regularizers.l1(0.01),
                kernel_constraint = constraints.MaxNorm(max_value=2, axis=0))) 
model.add(layers.Dense(10,
        kernel_regularizer=regularizers.l1_l2(0.01,0.01),activation = "sigmoid"))
model.compile(optimizer = "rmsprop",
        loss = "binary_crossentropy",metrics = ["AUC"])
model.summary()

内置损失函数
内置的损失函数一般有类的实现和函数的实现两种形式。

如：CategoricalCrossentropy 和 categorical_crossentropy 都是类别交叉熵损失函数，前者是类的实现形式，后者是函数的实现形式。

常用的一些内置损失函数说明如下。

1
2
3
4
5
6
7
8
9
10
mean_squared_error      # 均方误差损失，用于回归，简写为 mse, 类与函数实现形式分别为 MeanSquaredError 和 MSE
mean_absolute_error     # 平均绝对值误差损失，用于回归，简写为 mae, 类与函数实现形式分别为 MeanAbsoluteError 和 MAE
mean_absolute_percentage_error     # 平均百分比误差损失，用于回归，简写为 mape, 类与函数实现形式分别为 MeanAbsolutePercentageError 和 MAPE
Huber        # Huber损失，只有类实现形式，用于回归，介于mse和mae之间，对异常值比较鲁棒，相对mse有一定的优势
binary_crossentropy         # 二元交叉熵，用于二分类，类实现形式为 BinaryCrossentropy
categorical_crossentropy    # 类别交叉熵，用于多分类，要求label为onehot编码，类实现形式为 CategoricalCrossentropy
sparse_categorical_crossentropy    # 稀疏类别交叉熵，用于多分类，要求label为序号编码形式，类实现形式为 SparseCategoricalCrossentropy
hinge        # 合页损失函数，用于二分类，最著名的应用是作为支持向量机SVM的损失函数，类实现形式为 Hinge
kld          # 相对熵损失，也叫KL散度，常用于最大期望算法EM的损失函数，两个概率分布差异的一种信息度量。类与函数实现形式分别为 KLDivergence 或 KLD
cosine_similarity    # 余弦相似度，可用于多分类，类实现形式为 CosineSimilarity

高阶API

TensorFlow的高阶API主要是tensorflow.keras.models，包括

  • 模型的构建（Sequential、functional API、Model子类化）
  • 模型的训练（内置fit方法、内置train_on_batch方法、自定义训练循环、单GPU训练模型、多GPU训练模型、TPU训练模型）
  • 模型的部署（tensorflow serving部署模型、使用spark(scala)调用tensorflow模型）

构建模型

可以使用以下3种方式构建模型：使用Sequential按层顺序构建模型，使用函数式API构建任意结构模型，继承Model基类构建自定义模型。

  • 对于顺序结构的模型，优先使用Sequential方法构建。
  • 如果模型有多输入或者多输出，或者模型需要共享权重，或者模型具有残差连接等非顺序结构，推荐使用函数式API进行创建。
  • 如果无特定必要，尽可能避免使用Model子类化的方式构建模型，这种方式提供了极大的灵活性，但也有更大的概率出错。

下面以IMDB电影评论的分类问题为例，演示3种创建模型的方法。

使用Sequential按层顺序构建模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np 
import pandas as pd 
import tensorflow as tf
from tqdm import tqdm 
from tensorflow.keras import *


train_token_path = "../../data/imdb/train_token.csv"
test_token_path = "../../data/imdb/test_token.csv"

MAX_WORDS = 10000  # We will only consider the top 10,000 words in the dataset
MAX_LEN = 200  # We will cut reviews after 200 words
BATCH_SIZE = 20 

# 构建管道
def parse_line(line):
    t = tf.strings.split(line,"\t")
    label = tf.reshape(tf.cast(tf.strings.to_number(t[0]),tf.int32),(-1,))
    features = tf.cast(tf.strings.to_number(tf.strings.split(t[1]," ")),tf.int32)
    return (features,label)

ds_train=  tf.data.TextLineDataset(filenames = [train_token_path]) \
   .map(parse_line,num_parallel_calls = tf.data.experimental.AUTOTUNE) \
   .shuffle(buffer_size = 1000).batch(BATCH_SIZE) \
   .prefetch(tf.data.experimental.AUTOTUNE)

ds_test=  tf.data.TextLineDataset(filenames = [test_token_path]) \
   .map(parse_line,num_parallel_calls = tf.data.experimental.AUTOTUNE) \
   .shuffle(buffer_size = 1000).batch(BATCH_SIZE) \
   .prefetch(tf.data.experimental.AUTOTUNE)

Sequential按层顺序创建模型

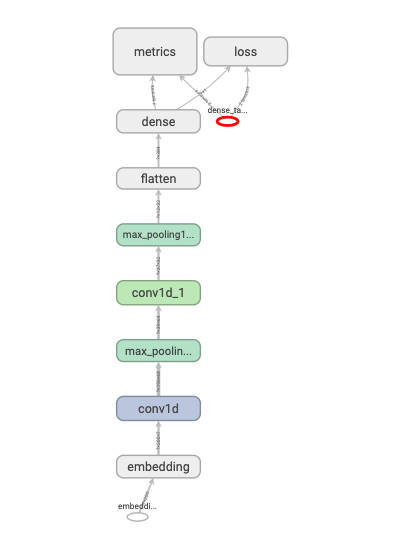
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tf.keras.backend.clear_session()

model = models.Sequential()

model.add(layers.Embedding(MAX_WORDS, 7, input_length=MAX_LEN))
model.add(layers.Conv1D(filters=64, kernel_size=5, activation="relu"))
model.add(layers.MaxPool1D(2))
model.add(layers.Conv1D(filters=32, kernel_size=3, activation="relu"))
model.add(layers.MaxPool1D(2))
model.add(layers.Flatten())
model.add(layers.Dense(1, activation = "sigmoid"))

model.compile(optimizer='Nadam',
            loss='binary_crossentropy',
            metrics=['accuracy',"AUC"])

model.summary()

函数式API创建任意结构模型

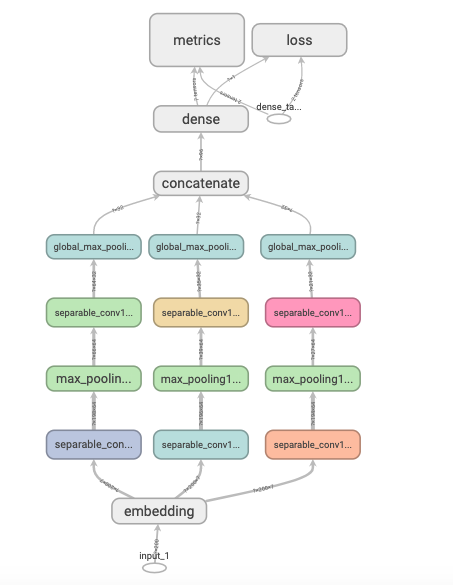
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
tf.keras.backend.clear_session()

inputs = layers.Input(shape=[MAX_LEN])
x  = layers.Embedding(MAX_WORDS, 7)(inputs)

branch1 = layers.SeparableConv1D(64, 3, activation="relu")(x)
branch1 = layers.MaxPool1D(3)(branch1)
branch1 = layers.SeparableConv1D(32,3,activation="relu")(branch1)
branch1 = layers.GlobalMaxPool1D()(branch1)

branch2 = layers.SeparableConv1D(64,5,activation="relu")(x)
branch2 = layers.MaxPool1D(5)(branch2)
branch2 = layers.SeparableConv1D(32,5,activation="relu")(branch2)
branch2 = layers.GlobalMaxPool1D()(branch2)

branch3 = layers.SeparableConv1D(64,7,activation="relu")(x)
branch3 = layers.MaxPool1D(7)(branch3)
branch3 = layers.SeparableConv1D(32,7,activation="relu")(branch3)
branch3 = layers.GlobalMaxPool1D()(branch3)

concat = layers.Concatenate()([branch1, branch2, branch3])
outputs = layers.Dense(1,activation = "sigmoid")(concat)

model = models.Model(inputs = inputs, outputs = outputs)

model.compile(optimizer='Nadam',
            loss='binary_crossentropy',
            metrics=['accuracy', "AUC"])

model.summary()

Model子类化创建自定义模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 先自定义一个残差模块，为自定义Layer

class ResBlock(layers.Layer):
    def __init__(self, kernel_size, **kwargs):
        super(ResBlock, self).__init__(**kwargs)
        self.kernel_size = kernel_size

    def build(self,input_shape):
        self.conv1 = layers.Conv1D(filters=64,kernel_size=self.kernel_size,
                                   activation = "relu",padding="same")
        self.conv2 = layers.Conv1D(filters=32,kernel_size=self.kernel_size,
                                   activation = "relu",padding="same")
        self.conv3 = layers.Conv1D(filters=input_shape[-1],
                                   kernel_size=self.kernel_size,activation = "relu",padding="same")
        self.maxpool = layers.MaxPool1D(2)
        super(ResBlock,self).build(input_shape) # 相当于设置self.built = True

    def call(self, inputs):
        x = self.conv1(inputs)
        x = self.conv2(x)
        x = self.conv3(x)
        x = layers.Add()([inputs,x])
        x = self.maxpool(x)
        return x

    #如果要让自定义的Layer通过Functional API 组合成模型时可以序列化，需要自定义get_config方法。
    def get_config(self):  
        config = super(ResBlock, self).get_config()
        config.update({'kernel_size': self.kernel_size})
        return config

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 自定义模型，实际上也可以使用Sequential或者FunctionalAPI

class ImdbModel(models.Model):
    def __init__(self):
        super(ImdbModel, self).__init__()

    def build(self,input_shape):
        self.embedding = layers.Embedding(MAX_WORDS,7)
        self.block1 = ResBlock(7)
        self.block2 = ResBlock(5)
        self.dense = layers.Dense(1,activation = "sigmoid")
        super(ImdbModel,self).build(input_shape)

    def call(self, x):
        x = self.embedding(x)
        x = self.block1(x)
        x = self.block2(x)
        x = layers.Flatten()(x)
        x = self.dense(x)
        return(x)

训练模型

模型的训练主要有内置fit方法、内置tran_on_batch方法、自定义训练循环。

注：fit_generator方法在tf.keras中不推荐使用，其功能已经被fit包含。

内置fit方法
该方法功能非常强大, 支持对numpy array, tf.data.Dataset以及 Python generator数据进行训练。并且可以通过设置回调函数实现对训练过程的复杂控制逻辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
tf.keras.backend.clear_session()
def create_model():

    model = models.Sequential()
    model.add(layers.Embedding(MAX_WORDS,7,input_length=MAX_LEN))
    model.add(layers.Conv1D(filters = 64,kernel_size = 5,activation = "relu"))
    model.add(layers.MaxPool1D(2))
    model.add(layers.Conv1D(filters = 32,kernel_size = 3,activation = "relu"))
    model.add(layers.MaxPool1D(2))
    model.add(layers.Flatten())
    model.add(layers.Dense(CAT_NUM,activation = "softmax"))
    return(model)

def compile_model(model):
    model.compile(optimizer=optimizers.Nadam(),
                loss=losses.SparseCategoricalCrossentropy(),
                metrics=[metrics.SparseCategoricalAccuracy(),metrics.SparseTopKCategoricalAccuracy(5)]) 
    return(model)

model = create_model()
model.summary()
model = compile_model(model)


history = model.fit(ds_train, validation_data=ds_test, epochs=10)

内置train_on_batch方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def create_model():
    model = models.Sequential()

    model.add(layers.Embedding(MAX_WORDS,7,input_length=MAX_LEN))
    model.add(layers.Conv1D(filters = 64,kernel_size = 5,activation = "relu"))
    model.add(layers.MaxPool1D(2))
    model.add(layers.Conv1D(filters = 32,kernel_size = 3,activation = "relu"))
    model.add(layers.MaxPool1D(2))
    model.add(layers.Flatten())
    model.add(layers.Dense(CAT_NUM,activation = "softmax"))
    return(model)

def compile_model(model):
    model.compile(optimizer=optimizers.Nadam(),
                loss=losses.SparseCategoricalCrossentropy(),
                metrics=[metrics.SparseCategoricalAccuracy(),metrics.SparseTopKCategoricalAccuracy(5)]) 
    return(model)

def train_model(model,ds_train,ds_valid,epoches):
    for epoch in tf.range(1,epoches+1):
        model.reset_metrics()

        # 在后期降低学习率
        if epoch == 5:
            model.optimizer.lr.assign(model.optimizer.lr/2.0)
            tf.print("Lowering optimizer Learning Rate...\n\n")

        for x, y in ds_train:
            train_result = model.train_on_batch(x, y)

        for x, y in ds_valid:
            valid_result = model.test_on_batch(x, y,reset_metrics=False)

        if epoch%1 ==0:
            printbar()
            tf.print("epoch = ",epoch)
            print("train:",dict(zip(model.metrics_names,train_result)))
            print("valid:",dict(zip(model.metrics_names,valid_result)))
            print("")

model = create_model()
model.summary()
model = compile_model(model)
train_model(model, ds_train, ds_test, 10)
文章作者: Dar1in9
文章链接: http://dar1in9s.github.io/2023/12/10/机器学习/tensorflow/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Dar1in9's Blog！